tidyfit is an R-package that facilitates and automates linear and nonlinear regression and classification modeling in a tidy environment. The package includes methods such as the Lasso, PLS, time-varying parameter or Bayesian model averaging regressions, and many more. The aim is threefold:
- Offer a standardized input-output interface for a broad set of “good” modeling packages. Unlike projects such as
caret, the aim is not to cover a comprehensive set of available packages, but rather a curated list of the most useful ones. - Efficient modeling with
tidydata, including verbs for regression and classification, automatic consideration of grouped data, andtidyoutput formats throughout. - Augment and automate methods to ensure statistical comparability (e.g. across coefficients of different linear estimators), sensible default settings, necessary transformations (e.g. standardizing features when required), automatic hyperparameter optimization, etc.
tidyfit builds on the tidymodels suite, but emphasizes automated modeling with a focus on grouped data, model comparisons, and high-volume analytics. The objective is to make model fitting, cross validation and model output very simple and standardized across all methods, with many necessary method-specific transformations handled in the background.
Installation
tidyfit can be installed from CRAN or the development version from GitHub with:
# CRAN
install.packages("tidyfit")
# Dev version
# install.packages("devtools")
devtools::install_github("jpfitzinger/tidyfit")
library(tidyfit)Overview and usage
tidyfit includes 3 deceptively simple functions:
All 3 of these functions return a tidyfit.models frame, which is a data frame containing information about fitted regression and classification models. regress and classify perform regression and classification on tidy data. The functions ingest a tibble, prepare input data for the models by splitting groups, partitioning cross validation slices and handling any necessary adjustments and transformations. The data is ultimately passed to the model wrapper m() which fits the models.
To illustrate basic usage, suppose we would like to fit a financial factor regression for 10 industries with exponential weighting, comparing a WLS and a weighted LASSO regression:
progressr::handlers(global=TRUE)
tidyfit::Factor_Industry_Returns %>%
group_by(Industry) %>% # Ensures that a model is fitted for each industry
mutate(Weight = 0.96^seq(n(), 1)) %>% # Exponential weights
# 'regress' allows flexible standardized regression analysis in a single line of code
regress(
Return ~ ., # Uses normal formula syntax
m("lasso"), # LASSO regression wrapper, 'lambda' grid set to default
m("lm"), # OLS wrapper (can add as many wrappers as necessary here)
.cv = "initial_time_split", # Cross-validation method for optimal 'lambda' in LASSO
.mask = "Date", # 'Date' columns should be excluded
.weights = "Weight" # Specifies the weights column
) -> models_df
# Get coefficients frame
coef(models_df)The syntax is identical for classify.
m is a powerful wrapper for many different regression and classification techniques that can be used with regress and classify, or as a stand-alone function:
m(
<method>, # e.g. "lm" or "lasso"
formula, data, # not passed when used within regress or classify
... # Args passed to underlying method, e.g. to stats::lm for OLS regression
)An important feature of m() is that all arguments can be passed as vectors, allowing generalized hyperparameter tuning or scenario analysis for any method:
- Passing a hyperparameter grid:
m("lasso", lambda = seq(0, 1, by = 0.1)) - Different algorithms for robust regression:
m("robust", method = c("M", "MM")) - Forward vs. backward selection:
m("subset", method = c("forward", "backward")) - Logit vs. Probit models:
m("glm", family = list(binomial(link="logit"), binomial(link="probit")))
Arguments that are meant to be vectors (e.g. weights) are recognized by the function and not interpreted as grids.
Methods implemented in tidyfit
tidyfit currently implements the following methods:
| Method | Name | Package | Regression | Classification |
|---|---|---|---|---|
| Linear (generalized) regression or classification | ||||
| OLS | lm |
stats
|
yes | no |
| GLS | glm |
stats
|
yes | yes |
| Robust regression (e.g. Huber loss) | robust |
MASS
|
yes | no |
| Quantile regression | quantile |
quantreg
|
yes | no |
| ANOVA | anova |
stats
|
yes | yes |
| Regression or classification with L1 and L2 penalties | ||||
| LASSO | lasso |
glmnet
|
yes | yes |
| Ridge | ridge |
glmnet
|
yes | yes |
| Group LASSO | group_lasso |
gglasso
|
yes | yes |
| Adaptive LASSO | adalasso |
glmnet
|
yes | yes |
| ElasticNet | enet |
glmnet
|
yes | yes |
| Machine Learning | ||||
| Gradient boosting regression | boost |
mboost
|
yes | yes |
| Support vector machine | svm |
e1071
|
yes | yes |
| Random forest | rf |
randomForest
|
yes | yes |
| Quantile random forest | quantile_rf |
quantregForest
|
yes | yes |
| Neural Network | nnet |
nnet
|
yes | no |
| Factor regressions | ||||
| Principal components regression | pcr |
pls
|
yes | no |
| Partial least squares | plsr |
pls
|
yes | no |
| Hierarchical feature regression | hfr |
hfr
|
yes | no |
| Subset selection | ||||
| Best subset selection | subset |
bestglm
|
yes | yes |
| Genetic Algorithm | genetic |
gaselect
|
yes | no |
| General-to-specific | gets |
gets
|
yes | no |
| Bayesian regression | ||||
| Bayesian regression | bayes |
arm
|
yes | yes |
| Bayesian Ridge | bridge |
monomvn
|
yes | no |
| Bayesian Lasso | blasso |
monomvn
|
yes | no |
| Bayesian model averaging | bma |
BMS
|
yes | no |
| Bayesian Spike and Slab | spikeslab |
BoomSpikeSlab
|
yes | yes |
| Bayesian time-varying parameters regression | tvp |
shrinkTVP
|
yes | no |
| Mixed-effects modeling | ||||
| Generalized mixed-effects regression | glmm |
lme4
|
yes | yes |
| Specialized time series methods | ||||
| Markov-switching regression | mslm |
MSwM
|
yes | no |
| Feature selection | ||||
| Pearson correlation | cor |
stats
|
no | no |
| Chi-squared test | chisq |
stats
|
yes | yes |
| Minimum redundancy, maximum relevance | mrmr |
mRMRe
|
yes | yes |
| ReliefF | relief |
CORElearn
|
yes | yes |
See ?m for additional information.
It is important to note that the above list is not complete, since some of the methods encompass multiple algorithms. For instance, “subset” can be used to perform forward, backward or exhaustive search selection using leaps. Similarly, “lasso” includes certain grouped LASSO implementations that can be fitted with glmnet.
A minimal workflow
In this section, a minimal workflow is used to demonstrate how the package works. For more detailed guides of specialized topics, or simply for further reading, follow these links:
- The flowchart
- Regularized regression (Boston house price data)
- Multinomial classification (iris data)
- Feature Selection (macroeconomic data)
- Accessing fitted models
- Rolling window regression for time series (factor data)
- Time-varying parameters (factor data)
- Bootstrap confidence intervals
tidyfit includes a data set of financial Fama-French factor returns freely available here. The data set includes monthly industry returns for 10 industries, as well as monthly factor returns for 5 factors:
data <- tidyfit::Factor_Industry_Returns
# Calculate excess return
data <- data %>%
mutate(Return = Return - RF) %>%
select(-RF)
data
#> # A tibble: 7,080 × 8
#> Date Industry Return `Mkt-RF` SMB HML RMW CMA
#> <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 196307 NoDur -0.76 -0.39 -0.44 -0.89 0.68 -1.23
#> 2 196308 NoDur 4.64 5.07 -0.75 1.68 0.36 -0.34
#> 3 196309 NoDur -1.96 -1.57 -0.55 0.08 -0.71 0.29
#> 4 196310 NoDur 2.36 2.53 -1.37 -0.14 2.8 -2.02
#> 5 196311 NoDur -1.4 -0.85 -0.89 1.81 -0.51 2.31
#> 6 196312 NoDur 2.52 1.83 -2.07 -0.08 0.03 -0.04
#> 7 196401 NoDur 0.49 2.24 0.11 1.47 0.17 1.51
#> 8 196402 NoDur 1.61 1.54 0.3 2.74 -0.05 0.9
#> 9 196403 NoDur 2.77 1.41 1.36 3.36 -2.21 3.19
#> 10 196404 NoDur -0.77 0.1 -1.59 -0.58 -1.27 -1.04
#> # ℹ 7,070 more rowsWe will only use a subset of the data to keep things simple:
df_train <- data %>%
filter(Date > 201800 & Date < 202000)
df_test <- data %>%
filter(Date >= 202000)Before beginning with the estimation, we can activate the progress bar visualization. This allows us to gauge estimation progress along the way. tidyfit uses the progressr-package internally to generate a progress bar — run progressr::handlers(global=TRUE) to activate progress bars in your environment.
For purposes of this demonstration, the objective will be to fit an ElasticNet regression for each industry group, and compare results to a robust least squares regression. This can be done with regress after grouping the data. For grouped data, the functions regress and classify estimate models for each group independently:
model_frame <- df_train %>%
group_by(Industry) %>%
regress(Return ~ .,
m("enet"),
m("robust", method = "MM", psi = MASS::psi.huber),
.cv = "initial_time_split", .mask = "Date")Note that the penalty and mixing parameters are chosen automatically using a time series train/test split (rsample::initial_time_split), with a hyperparameter grid set by the package dials. See ?regress for additional CV methods. A custom grid can easily be passed using lambda = c(...) and/or alpha = c(...) in the m("enet") wrapper.
The resulting tidyfit.models frame consists of 3 components:
- A group of identifying columns. This includes the
Industrycolumn, the model name, and grid ID (the ID for the model settings used). -
estimator_fct,size (MB)andmodel_objectcolumns. These columns contain information on the model itself. Themodel_objectis the fittedtidyFitmodel (anR6class that contains the model object as well as any additional information needed to perform predictions or access coefficients) - Nested
settings, as well as (if applicable)messagesandwarnings.
subset_mod_frame <- model_frame %>%
filter(Industry %in% unique(Industry)[1:2])
subset_mod_frame
#> # A tibble: 4 × 8
#> Industry model estimator_fct `size (MB)` grid_id model_object settings
#> <chr> <chr> <chr> <dbl> <chr> <list> <list>
#> 1 Enrgy enet glmnet::glmnet 1.21 #001|100 <tidyFit> <tibble>
#> 2 Shops enet glmnet::glmnet 1.21 #001|049 <tidyFit> <tibble>
#> 3 Enrgy robust MASS::rlm 0.0638 #0010000 <tidyFit> <tibble>
#> 4 Shops robust MASS::rlm 0.0638 #0010000 <tidyFit> <tibble>
#> # ℹ 1 more variable: warnings <chr>Let’s unnest the settings columns:
subset_mod_frame %>%
tidyr::unnest(settings, keep_empty = TRUE)
#> # A tibble: 4 × 13
#> Industry model estimator_fct `size (MB)` grid_id model_object alpha weights
#> <chr> <chr> <chr> <dbl> <chr> <list> <dbl> <list>
#> 1 Enrgy enet glmnet::glmnet 1.21 #001|100 <tidyFit> 0 <NULL>
#> 2 Shops enet glmnet::glmnet 1.21 #001|049 <tidyFit> 0 <NULL>
#> 3 Enrgy robust MASS::rlm 0.0638 #0010000 <tidyFit> NA <NULL>
#> 4 Shops robust MASS::rlm 0.0638 #0010000 <tidyFit> NA <NULL>
#> # ℹ 5 more variables: family <chr>, lambda <dbl>, method <chr>, psi <list>,
#> # warnings <chr>The tidyfit.models frame can be used to access additional information. Specifically, we can do 4 things:
- Access the fitted model
- Predict
- Access a data frame of estimated parameters
- Use additional generics
The fitted tidyFit models are stored as an R6 class in the model_object column and can be addressed directly with generics such as coef or summary. The underlying object (e.g. an lm class fitted model) is given in ...$object (see here for another example):
subset_mod_frame %>%
mutate(fitted_model = map(model_object, ~.$object))
#> # A tibble: 4 × 9
#> Industry model estimator_fct `size (MB)` grid_id model_object settings
#> <chr> <chr> <chr> <dbl> <chr> <list> <list>
#> 1 Enrgy enet glmnet::glmnet 1.21 #001|100 <tidyFit> <tibble>
#> 2 Shops enet glmnet::glmnet 1.21 #001|049 <tidyFit> <tibble>
#> 3 Enrgy robust MASS::rlm 0.0638 #0010000 <tidyFit> <tibble>
#> 4 Shops robust MASS::rlm 0.0638 #0010000 <tidyFit> <tibble>
#> # ℹ 2 more variables: warnings <chr>, fitted_model <list>To predict, we need data with the same columns as the input data and simply use the generic predict function. Groups are respected and if the response variable is in the data, it is included as a truth column in the resulting object:
predict(subset_mod_frame, data)
#> # A tibble: 2,832 × 4
#> # Groups: Industry, model [4]
#> Industry model prediction truth
#> <chr> <chr> <dbl> <dbl>
#> 1 Enrgy enet -3.77 2.02
#> 2 Enrgy enet 3.90 3.69
#> 3 Enrgy enet -2.40 -3.91
#> 4 Enrgy enet -3.30 -0.61
#> 5 Enrgy enet 0.762 -1.43
#> 6 Enrgy enet -0.293 4.36
#> 7 Enrgy enet 3.68 4.54
#> 8 Enrgy enet 2.31 0.8
#> 9 Enrgy enet 7.26 1.09
#> 10 Enrgy enet -2.53 3.74
#> # ℹ 2,822 more rowsFinally, we can obtain a tidy frame of the coefficients using the generic coef function:
estimates <- coef(subset_mod_frame)
estimates
#> # A tibble: 24 × 5
#> # Groups: Industry, model [4]
#> Industry model term estimate model_info
#> <chr> <chr> <chr> <dbl> <list>
#> 1 Enrgy enet (Intercept) -0.955 <tibble [1 × 4]>
#> 2 Enrgy enet Mkt-RF 1.20 <tibble [1 × 4]>
#> 3 Enrgy enet SMB 0.703 <tibble [1 × 4]>
#> 4 Enrgy enet HML -0.00208 <tibble [1 × 4]>
#> 5 Enrgy enet RMW -0.622 <tibble [1 × 4]>
#> 6 Enrgy enet CMA 1.32 <tibble [1 × 4]>
#> 7 Shops enet (Intercept) 1.03 <tibble [1 × 4]>
#> 8 Shops enet Mkt-RF 0.0849 <tibble [1 × 4]>
#> 9 Shops enet SMB 0.0353 <tibble [1 × 4]>
#> 10 Shops enet HML -0.0149 <tibble [1 × 4]>
#> # ℹ 14 more rowsThe estimates contain additional method-specific information that is nested in model_info. This can include standard errors, t-values and similar information:
tidyr::unnest(estimates, model_info)
#> # A tibble: 24 × 8
#> # Groups: Industry, model [4]
#> Industry model term estimate lambda dev.ratio std.error statistic
#> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 Enrgy enet (Intercept) -0.955 0.536 0.812 NA NA
#> 2 Enrgy enet Mkt-RF 1.20 0.536 0.812 NA NA
#> 3 Enrgy enet SMB 0.703 0.536 0.812 NA NA
#> 4 Enrgy enet HML -0.00208 0.536 0.812 NA NA
#> 5 Enrgy enet RMW -0.622 0.536 0.812 NA NA
#> 6 Enrgy enet CMA 1.32 0.536 0.812 NA NA
#> 7 Shops enet (Intercept) 1.03 50.1 0.173 NA NA
#> 8 Shops enet Mkt-RF 0.0849 50.1 0.173 NA NA
#> 9 Shops enet SMB 0.0353 50.1 0.173 NA NA
#> 10 Shops enet HML -0.0149 50.1 0.173 NA NA
#> # ℹ 14 more rowsAdditional generics such as fitted or resid can be used to obtain more information on the models.
Suppose we would like to evaluate the relative performance of the two methods. This becomes exceedingly simple using the yardstick package:
model_frame %>%
# Generate predictions
predict(df_test) %>%
# Calculate RMSE
yardstick::rmse(truth, prediction) %>%
# Plot
ggplot(aes(Industry, .estimate)) +
geom_col(aes(fill = model), position = position_dodge())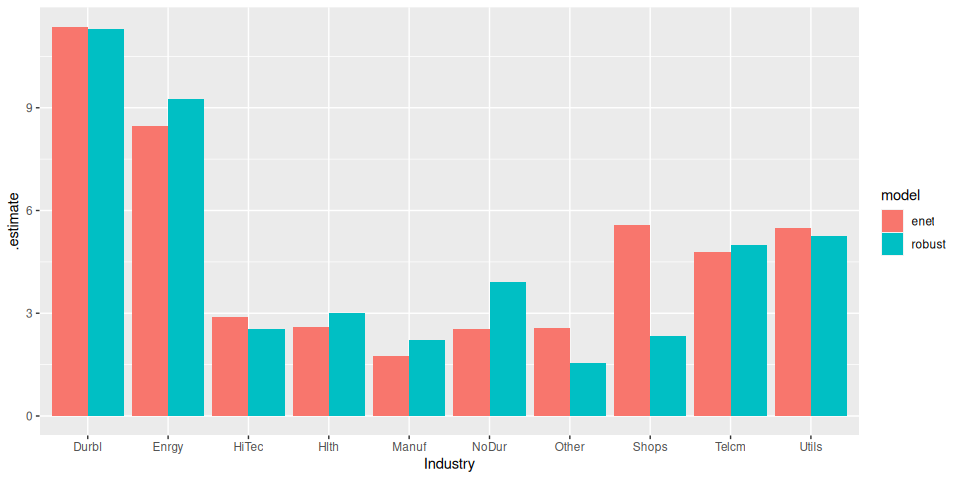
The ElasticNet performs a little better (unsurprising really, given the small data set).
A more detailed regression analysis of Boston house price data using a panel of regularized regression estimators can be found here.

